So, you've written your code carefully, or copied it from a book, and compiled it without any error messages, but it doesn't run, or it does run and does something you didn't intend or expect. You have tried desk-checking the program in the light of its behavior, and you just can't see what is wrong with it. You need to debug it. Unfortunately, many courses on programming spend little or no time on teaching the art of debug. Debuggers often come with tutorials on how to use them in the sense of what to do if you have decided you need a break point at a particular line.
This article is about the other end of the problem, deciding what information to collect at what points in the program, and how to use that information to decide what to do next. It attempts to explain an approach to debug that I have found to be very effective.
While the example is a short, simple Java application, I have successfully applied the high level concepts to extremely difficult intermittent bugs in multithreaded, multiprocessor programs and in prototypes of multiprocessor computers. The approach is a completely general one, independent of the tools you are using. It may be difficult to follow the example if you don't read Java, but the rest of the article is independent of programming language.
You will also need some way of obtaining information about the states of variables as selected points in the program run. How you will do this depends on the language and tools you are using. For small programs that compile and run in seconds it may be a simple as inserting extra display statements in the source code. Debuggers can also be used for these cases, but are especially useful when making a change, compiling, and running to the point of failure takes several minutes or longer.
Terminology note: The word "theory" is used here for any proposed explanation
of the causes and structure behind some observations, covering everything
from a totally untested hypothesis through a mathematically proved theorem.
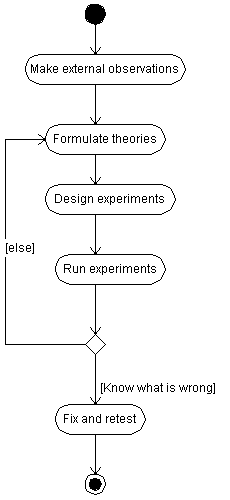
The essence of this technique is a simple sequence of steps that starts after a bug has been selected for debug, and ends when it has been fixed. In the middle there is a loop that improves information about the bug.

Programming is usually more successful if done in steps, with each step focussed on a limited readily achievable objective. In the same way, all except the simplest of debug tasks should be done in steps, with each step focussed on forming the next set of questions. It is not necessary, and often not possible, to get to the root cause in one step. Progress is being made as long as possibilities are eliminated or the theories become more specific, a little closer to identifying the root cause.
An alternative approach is to wait for a sudden insight in which you just realize where the problem lies. For example, many programmers have had the experience of going to sleep thinking about a bug and waking up knowing the solution. Insights are fine, and should always be checked out. They may save a lot of time. However, insights don't always appear when needed. While waiting for one to strike, it is a good idea to pursue an organized approach that will inevitably find the bug.
For relatively small pieces of code, bugs can often be found by simply reading the code in the belief that it contains errors. Even in larger programs, code inspection can be very effective, and save time, once the bug has been narrowed down to a manageable area. If the bug appeared while the program is being modified there is an increased chance that the problem is in the changed code or things with which it interacts. In that case a review of those areas may be appropriate.
This preparatory step can be surprisingly important.
It is important to know whether the program always produces the same results, given the same input. If this is not the case great care is needed in interpreting results. It may be necessary to run tests several times, and even apply statistical techniques to the results. Multithreaded programs are more likely to have varying behavior.
In many cases it is helpful to run several tests to see what, if anything, affects the program's behavior. It is usually best to base a debug effort on the shortest and simplest case that fails. Knowing cases that work may help constrain the initial theories.
There are two slightly different cases. During the first iteration the theories have to be based on the external observations and simple conclusions from the source code. During the second and subsequent iterations, there is also a body of existing theories that have been tested to some extent.
In many cases it is possible to formulate a set of theories at least one of which MUST be true.
For example, consider the first iteration when the symptom is a NullPointerException. There will be a limited set of expressions in the line throwing the exception that are used to identify objects. At least one of those expressions must be null.
On second and subsequent iterations the main source of theories is going to be refinement of the theories from the previous iteration. However, unless you are absolutely certain that you have a case where at least one of those theories must be true, you should also consider adding new theories based on the current observations. This is unavoidable if you have succeeded in disproving all your previous theories.
A good theory makes testable predictions. Truth of all predictions made by a theory does not in itself prove the theory to be correct. Falsity of any prediction disproves the theory, at least in its current form. Of course, given a sufficiently precise, detailed theory about a computer program, it is often possible to prove its truth by examining the code.
If two theories make differing predictions for the outcome of the same experiment that experiment must disprove at least one of them. Such experiments are especially valuable and should be given high priority.
Sometimes there is a whole spectrum of related theories. Suppose you know that a variable had the correct value at point A in the program run, had a different value at point B, and according to the program design should not change between A and B. There is in a sense a separate theory available for every line of code reached between A and B, asserting that that particular line of code on that occasion changed the value.
There are several reasonable approaches; exhaustive, work forwards, work backwards, and binary search. If the number of iterations is small, use an exhaustive approach in which you trace the value on every iteration. Forwards experiments work forwards from point A, testing whether the value is still correct. Backwards experiments look shortly before point B, looking for the last point at which the variable was correct. Binary search tests the variable at a point half way between A and B. If the value is correct there, move to a point half way between there and B. If it is incorrect, look next half way between A and the tested point.
One good approach is to try a few tests close to each of A and B. If the value is consistently good close to A, and consistently bad close to B, then switch to a binary search.
In all cases, the objective to is bracket the change in the variable by narrowing the range between the latest point at which the variable is known to be good and the earliest point at which it is known to be bad.
Another useful experimental technique is removal of code. Obviously, before embarking on major source code surgery you should make sure you have back-up copies of the original and/or have it under revision control. If you have a theory that a portion of the code is irrelevant, delete that portion or replace it with a simple stub.
If the problem is a complicated one, keep written notes of experiments run, their results, and conclusions. Even if the program appears to have repeatable behavior, periodically do the same experiment twice to check that there are no differences.
This is the only part of the process where the choice of debugging tool makes much difference.
Considering the results of all the experiments so far, it is possible that the problem is now sufficiently constrained that it can be found by examining the code. If so, the debug effort is effectively complete.
Sometimes, it may not be clear whether the debug effort is over or not. For example, suppose you have determined that a particular variable is null at a time when it is being used to reference an object. There are three cases:
Fix the bug that has been identified. Also, consider its possible implications
for the rest of the program. Is this particular bug indicative of a general problem that may affect other places in the code? Were there omissions in unit testing that let an erroneous component get integrated into the program?
Several types of testing should be done:
Some programs will behave differently on repeated runs given identical inputs. These can be the hardest bugs to find and fix. They are sometimes known as "Heisenbugs" after Heisenberg's Uncertainty Principle. Attempts to observe them often change their behavior.
The simplest and easiest approach, at least in the short term, is denial. Refuse to debug unless the user can provide a test case that reliably reproduces the bug. Reject bug reports with "unable to reproduce". This approach is very popular, except with people who have to use the programs.
The second simplest approach is to add arbitrary synchronization until the bug goes away. This has some serious disadvantages; it may only reduce the frequency of the bug, it may cause deadlocks, and it may reduce performance. Reducing the frequency of the bug is often not a long term solution because any production system will clock a lot more time being used than being tested. A bug whose frequency is too low for it to have much chance of appearing during testing may still be a serious problem for customers.
The hardest approach, but the most effective in the long term, is to actually debug them. The same basic system works, with a few differences:
Suppose a problem has been narrowed down to a few lines of code, and what the code is doing is not what was expected. One possibility is that there is a bug in the language implementation. However, most of the time the error will be in the programmer's interpretation. Here is a series of steps that can resolve this:
I have written a short program to solve a common student exercise. There are bugs in it. Please do not attempt to find them by code inspection. Pretend that the program is too big for that.
/** Solve a common student exercise - display the primes from 2 up to a specified limit. */ public class Example{ public static void main(String[] args){ //Find and print primes up to args[0]. //Convert and validate the command line argument if(args.length < 1){ System.err.println("Usage: java Example max"); System.exit(3); } int max=0; try{ max = Integer.parseInt(args[0]); }catch(NumberFormatException e){ e.printStackTrace(); System.exit(2); } if(max < 2){ System.err.println( "Maximum prime to look for must be 2 or greater"); System.exit(1); } // Get the required primes in an array PrimeFinder pf = new PrimeFinder(); int[] primes = pf.getPrimes(max); // Print them. for(int i=0;i<primes.length;i++){ System.out.println(primes[i]); } } } /** Prime number finder. */ class PrimeFinder{ /** Get the primes. @return An array containing the primes from 2 through the largest prime less than or equal to max. @param max The upper bound of the range to search for primes. */ int[] getPrimes(int max){ /* Use sieve method to eliminate all numbers that are divisible by 2 through sqrt(count). */ /* Sieve set - all composite numbers in the range 2 through max will be represented in this set. */ FixedSizedBitSet sieve = new FixedSizedBitSet(max+1); /* The primes, will contain the values in the range 2 through max that have not been found to be composite. */ FixedSizedBitSet results = new FixedSizedBitSet(max+1); /* All composite numbers less than or equal to max will have at least one factor less than or equal to stop. */ int stop = (int)Math.sqrt(max); /* First do the sieving - add all composite numbers in the range to sieve set. */ for(int i=2;i<stop;i++){ if(!sieve.contains(i)){ for(int j=2*i;j<=max;j+=i){ sieve.add(j); } } } /* Now find the numbers in the range that are not in the sieve set. */ for(int i=2;i<=max;i++){ if(!sieve.contains(i)){ results.add(i); } } return results.toIntArray(); } } /** Simple bit set for pre-determined sizes. */ class FixedSizedBitSet{ long[] bits; int elems; // number of potential elements /** Create a set based on a specified number of potential elements. The elements will be indexed 0 through elems-1. @param elems Number of potential elements */ FixedSizedBitSet(int elems){ this.elems = elems; bits = new long[(elems+63)/64]; } /** Add a specified element to the set @param elem Element number to add */ void add(int elem) throws IllegalArgumentException{ if(elem >= elems || elem < 0){ throw new IllegalArgumentException(); } bits[elem/64] |= mask(elem); } /** Remove a specified element from the set @param elem Element number to remove */ void remove(int elem)throws IllegalArgumentException{ if(elem >= elems || elem < 0){ throw new IllegalArgumentException(); } bits[elem/64] &= ~mask(elem); } /** Test whether a specified element is in the set. @param elem The element to set @return true if it is present, false if it is absent */ boolean contains(int elem){ boolean result=false; if(elem < 0 || elem >= elems){ return false; } return (bits[elem/64] & mask(elem))!=0; } /** Construct a mask with only the bit corresponding to the element number on. @param elem The element number */ private long mask(int elem){ return 1 << (elem %64); } /** Return int[] representation. @return An int[] containing the element numbers that are currently in this set, in ascending order */ int[] toIntArray(){ // Count the elements in the set. int count=0; for(int i=0;i<elems;i++){ if(contains(i)){ count++; } } // Create an array to contain that number of elements int[] results = new int[count]; // Fill in the ones that are in the set. int j = 0; for(int i=0;i<elems;i++){ if(contains(i)){ results[j] = i; j++; } } return results; } }
This version works correctly for command line parameters 2 and 3, but for 4 it displays:
2 3 4
falsely reporting that 4 is a prime. This is the first bug that will be analyzed.
The known failing case is a small and simple one. However, it is still worth doing some more experiments to find out which values fail. 4, 5, 6, 7, and 8 all show similar symptoms, with all numbers from 2 through the limit being listed as primes. 9, on the other hand, reports:
2 3 5 7 9
The values are correct, except for the inclusion of 9. Behavior changed at parameter values 4 and 9. These are both perfect squares, raising the issue of what happens around 16, the next square. 15 gives correct answers except for listing 9 and 15 as squares. 16 got completely correct results.
Nothing obvious here, but keep in mind the possibility that squares have some significance. Meanwhile, 4 is the smallest and simplest failing case and will be debugged.
There are two ways a wrong answer can be in the result set. Either it was
added by the PrimeFinder or it was due to an error in
FixedSizedBitSet.
Add code to PrimeFinder to display elements being added to the result set:
for(int i=2;i<=max;i++){
if(!sieve.contains(i)){
System.out.println("Adding "+i);
results.add(i);
}
}
Adding 2 Adding 3 Adding 4 2 3 4
The theory that 4 is being added by PrimeFinder is supported, and the theory
that it was appearing due to a bug in FixedSizedBitSet is disproved. There
is insufficient information to fix the bug at this point, so continue debug
effort.
I now have a well supported theory, that PrimeFinder is adding 4 to the
result set in the loop where it also adds the correct result elements.
New theories should be based on refining that one. It appears that 4 may
have been absent from the sieve, not marked as a composite in the sieve
loop.
Move the display code to the sieve loop to see whether 4 is detected there as a composite number:
for(int i=2;i<stop;i++){
if(!sieve.contains(i)){
for(int j=2*i;j<=max;j+=i){
System.out.println("Adding "+j);
sieve.add(j);
}
}
}
The new output is:
2 3 4
Because of the lack of any debug output at all, check the output statement, but it appears to be correct. In a more complicated case, I would test other values, to verify the output statement or breakpoint, before fully accepting an absence of output as valid data.
This is an interesting result. It matches the final result in showing
that no numbers are detected as composite. On the other hand, I know the
loop can find composites because of other tests. I would have expected
4 to be eliminated when i is 2 in the outer loop. However, i will not take
the value 2. For max=4, stop should itself take the value 2, and the loop
continuation condition is i<stop. This is the bug.
It is consistent with the other wrong answers under consideration. It will cause failure to sieve out composite numbers whose smallest prime factor is equal to stop, the largest int less that or equal to the square root of max. For 4 through 8, stop will be 2, and even numbers will be missed. For 9, stop is 3, and 9 will be missed. Perfect squares are significant.
Change the loop continuation condition from
i<stop to i<=stop.
Test that the current cases are fixed. It is. Parameter 4 now gets 2 and 3 as output. Also the other failing cases such as 9 now get correct results.
Next, regression test previously working cases. Cases 2 and 3 still get correct results.
Finally, extend testing to additional cases. Since the FixedSizedBitSet
deals with block of 64 bits, 64 and values greater than 64 are obviously
interesting. 64 gets:
5 11 17 29 37 43 49 61
This is obviously broken. There are many primes missing, although almost all reported values are prime. I wonder what happens for 32?
2 3 5 7 11 13 17 19 23 29 31
Looks good. How about 48?
5 11 17 19 23 29 31 37 43
Not so good. Try 40:
5 11 13 17 19 23 29 31 37
Also bad, and similar to 48.
36?
5 7 11 13 17 19 23 29 31
34?
3 5 7 11 13 17 19 23 29 31
Two is missing. 33?
2 3 5 7 11 13 17 19 23 29 31
All correct.
It is possible, though by no means certain, that 34 is the smallest failing case. Pick that as the one to debug. Note that the problem seems to get worse with increasing size of the parameter.
The failure of 2 to appear in the result set could either be an error in
the result set handling or a failure by PrimeFinder to put it in the result
set.
Put back in the first debug statement, tracing additions to the result set.
Adding 3 Adding 5 Adding 7 Adding 11 Adding 13 Adding 17 Adding 19 Adding 23 Adding 29 Adding 31 3 5 7 11 13 17 19 23 29 31
Looks as though 2 was never added to the result set.
That could be because it had been falsely picked up by the sieve, so that
the !sieve.contains(i) test failed, or because the loop doesn't test 2,
or because of an error in FixedSizedBitSet.
The first two theories can be tested by adding display code to PrimeFinder:
/* First do the sieving - add all composite numbers in the range to sieve set. */ for(int i=2;i<stop;i++){ if(!sieve.contains(i)){ for(int j=2*i;j<=max;j+=i){ System.out.println("Sieved out "+j); sieve.add(j); } } } /* Now find the numbers in the range that are not in the sieve set. */ for(int i=2;i<=max;i++){ System.out.println("Testing "+i); if(!sieve.contains(i)){ results.add(i); } }
Sieved out 4 Sieved out 6 Sieved out 8 Sieved out 10 Sieved out 12 Sieved out 14 Sieved out 16 Sieved out 18 Sieved out 20 Sieved out 22 Sieved out 24 Sieved out 26 Sieved out 28 Sieved out 30 Sieved out 32 Sieved out 34 Sieved out 6 Sieved out 9 Sieved out 12 Sieved out 15 Sieved out 18 Sieved out 21 Sieved out 24 Sieved out 27 Sieved out 30 Sieved out 33 Sieved out 10 Sieved out 15 Sieved out 20 Sieved out 25 Sieved out 30 Testing 2 Testing 3 Testing 4 Testing 5 Testing 6 Testing 7 Testing 8 Testing 9 Testing 10 Testing 11 Testing 12 Testing 13 Testing 14 Testing 15 Testing 16 Testing 17 Testing 18 Testing 19 Testing 20 Testing 21 Testing 22 Testing 23 Testing 24 Testing 25 Testing 26 Testing 27 Testing 28 Testing 29 Testing 30 Testing 31 Testing 32 Testing 33 Testing 34 3 5 7 11 13 17 19 23 29 31
2 was not added to the sieve set, was tested by the second loop, but at that time was reported as being in the sieve set.
At some point 2 must have appeared in the set. This includes the possibility that the set was not initially empty. There are three families of theories, it was always there, it appeared during the first loop, and it appeared during the second loop.
Display the truth of the expression sieve.contains(2)
before each of the two loops:
System.out.println("Before first loop "+sieve.contains(2));
/* First do the sieving - add all composite numbers
in the range to sieve set. */
for(int i=2;i<stop;i++){
if(!sieve.contains(i)){
for(int j=2*i;j<=max;j+=i){
sieve.add(j);
}
}
}
System.out.println("Between loops "+sieve.contains(2));
Before first loop false Between loops true
[From here on, the non-debug output is dropped to save space].
2 somehow got into the sieve set during the first loop, but without being explicitly added.
There is a whole family of theories, one for each iteration of the first loop.
If the loop did more iterations, I might do a binary search for when 2 got into the set. As it is, I'm just going to display the truth of the contains expression on each iteration:
for(int i=2;i<stop;i++){
System.out.println("Start i="+i+" "+sieve.contains(2));
if(!sieve.contains(i)){
for(int j=2*i;j<=max;j+=i){
sieve.add(j);
}
}
System.out.println("End i="+i+" "+sieve.contains(2));
}
Start i=2 false End i=2 true Start i=3 true End i=3 true Start i=4 true End i=4 true Start i=5 true End i=5 true
2 got into the sieve set during the first iteration of the outer loop of the sieve.
Again, it could have appeared before the inner loop, during any iteration of the inner loop, or after the inner loop was done.
Move the output statements into the inner loop, but modified to make them conditional on being on the i=2 iteration of the outer loop:
for(int j=2*i;j<=max;j+=i){
if(i==2){
System.out.println("Start j="+j+" "+sieve.contains(2));
}
sieve.add(j);
if(i==2){
System.out.println("End j="+j+" "+sieve.contains(2));
}
}
Start j=4 false End j=4 false Start j=6 false End j=6 false Start j=8 false End j=8 false Start j=10 false End j=10 false Start j=12 false End j=12 false Start j=14 false End j=14 false Start j=16 false End j=16 false Start j=18 false End j=18 false Start j=20 false End j=20 false Start j=22 false End j=22 false Start j=24 false End j=24 false Start j=26 false End j=26 false Start j=28 false End j=28 false Start j=30 false End j=30 false Start j=32 false End j=32 false Start j=34 false End j=34 true
2 appeared in the sieve set during the j=34 iteration of the inner loop.
The obvious theory is that somehow attempting to add 34 to the set added 2. It could be in addition to, or instead of, 34.
Modify the display code to focus on the j=34 iteration, and display the
state of 34 as well as 2:
for(int j=2*i;j<=max;j+=i){
if(i==2 && j==34){
System.out.println("Start 2 "+sieve.contains(2)+
" 34 "+sieve.contains(34));
}
sieve.add(j);
if(i==2 && j==34){
System.out.println("End 2 "+sieve.contains(2)+
" 34 "+sieve.contains(34));
}
}
Start 2 false 34 false End 2 true 34 true
Both 2 and 34 were added.
At this point attention shifts to inside the FixedSizedBitSet implementation.
A single "add" call should only add one element to the set, but appears
to have caused the contains() result for both 2 and 34 to change to true.
Looking at the add code in FixedSizedBitSet, it appears that the problem
is unlikely to be selection of the wrong array element since 34 and two
should both be represented in element 0. The best theory to test next seems
to be that the mask is wrong.
There are two approaches at this point. Normally, I would put a pure utility
class like FixedSizedBitSet in its own file, and unit test it by itself.
This would be an easier approach. However, in order to illustrate techniques,
I'm going to continue to debug it in the whole program.
Delete the existing debug outputs, and modify FixedSizedBitSet's
add
method to display the mask when working on element 34:
void add(int elem) throws IllegalArgumentException{ if(elem >= elems || elem < 0){ throw new IllegalArgumentException(); } bits[elem/64] |= mask(elem); if(elem == 34){ System.out.println("mask "+ Long.toBinaryString(mask(elem))); } }
mask 100
Bit 2 is on, and bit 34 is off. Clearly, the problem is in the
mask calculation.
The mask calculation:
return 1 << (elem %64);
is obviously incorrect. Because 1 is an int the shift will be done in 32
bit int arithmetic, and will wrap around. An attempted 34 bit shift will
actually shift by 2 bits. More generally, each time the
PrimeFinder tried
to sieve out a number n in the range 32 through 63 it would actually sieve
out n-32. This explains worse results from larger numbers.
The fix is to change the 1 to 1L, the long literal with the same value.
The problem case 34, other cases that had been previously tested, and several additional tests, all now give correct results.
Omitting the argument, and invalid numeric values such as 1, 0, and -1, all gave reasonable error messages. However, testing "ssss" got:
java.lang.NumberFormatException: ssss
at java.lang.Integer.parseInt(Integer.java:409)
at java.lang.Integer.parseInt(Integer.java:458)
at Example.main(Example.java:15)
Although the parameter value is incorrect, a raw exception is not a good way of handling a user input error. This requires little or no debug - it just needs a modification to the catch block in the main method.
Each bug was tracked down to the statement that caused it without any great leaps of insight, just steady cutting away at the scope of the problem.